Skip to contents

IES_Simulation

Source: vignettes/articles/IES_Simulation.Rmd
IES_Simulation.Rmd

Test the compilation environment.

Since this brochure is built from a github remote server, let’s first test the setup of the server. I’ll write a small snippet of code here to check if it works on the github remote server. Mainly because mclapply doesn’t run on windows, in addition to testing to see if parallel computation is possible and estimating the running time.

Nonparallel: 

data <- data_IES_Case_1_Train
start_time <- Sys.time()
result <- lapply(1:50000, function(x) lm(y ~. , data = data)[["coefficients"]][1])
print(Sys.time() -  start_time)
#> Time difference of 1.648098 mins

Parallel with 2 cores: 

data <- data_IES_Case_1_Train
start_time <- Sys.time()
result <- mclapply(1:50000, function(x) lm(y ~. , data = data)[["coefficients"]][1], mc.cores = 2)
print(Sys.time() -  start_time)
#> Time difference of 52.93846 secs

Parallel with 5 cores: 

data <- data_IES_Case_1_Train
start_time <- Sys.time()
result <- mclapply(1:50000, function(x) lm(y ~. , data = data)[["coefficients"]][1], mc.cores = 5)
print(Sys.time() -  start_time)
#> Time difference of 40.82492 secs

We don’t know how many cores the remote server can assign us. After trying, the remote server did assign us multiple cores, and five cores seemed to be the fastest and most locally appropriate number.

Implement with R or Rcpp

Seed Setting

IES is not a absolutely deterministic sampling method, pay attention to the setting of random seeds.

Compare Running Time

We have some problem in setting random seed between R and C++, so we cannot directly check whether the results of R and Rcpp are same. If we change all the random steps to pick the first element(r_IES_compare and c_IES_compare), we get the same result of R and Rcpp, this proves the correctness of the codes. We can compare the running time of R and Rcpp (In fact is RcppArmadillo):

X_compare <- dbsubsampling::data_IES_Case_1_Train[, c("X1", "X2", "X3")]
n <- 1000; q <- 16;

bench_result <- bench::mark(
  dbsubsampling::r_IES_compare(X_compare, n, q),
  dbsubsampling::c_IES_compare(X_compare, n, q),
  iterations = 10
)
bench_result[c("expression", "min", "median", "mem_alloc", "n_gc")]
#> # A tibble: 2 × 4
#>   expression                                         min   median mem_alloc
#>   <bch:expr>                                    <bch:tm> <bch:tm> <bch:byt>
#> 1 dbsubsampling::r_IES_compare(X_compare, n, q)    19.7s    19.7s     1.1GB
#> 2 dbsubsampling::c_IES_compare(X_compare, n, q)  109.4ms    110ms    1.52MB

RcppArmadillo greatly improves speed. We use RcppArmadillo in the main function.

Addition compare

The authors of IES wrote a sampling program in python, and we roughly compare:

reticulate::source_python("/Users/jie/Desktop/IES/IES_supp/ies.py")
get.lat= function(x, snew=16) { 
  s0=max(x)-min(x)
  lat=floor((x-min(x))/(s0/snew))
  lat[lat==snew]=snew-1
  lat
}
py_IES <- function(x, k){
  xl=apply(x,2,get.lat)
  n = nrow(x)
  initial=c(sample(1:n,1))
  ies=Uclab(xl,k,ini=initial-1)+1 
  return(ies)
}
system.time(lapply(1:10, function(i) py_IES(X_case1,n))) 
# user     system   elapsed 
# 2.506    0.435    2.956
system.time(lapply(1:10, function(i) c_IES(X_case1,n,q=16)))
# user     system   elapsed 
# 0.374    0.001    0.376 
system.time(lapply(1:10, function(i) r_IES(X_case1,n,q=16)))
# user     system   elapsed 
# 77.587   0.665    78.636

We can see that python is not as fast as C++, but much faster than R. (The reason we simply output the results without running this code is because of the complexity of the additional setup required to use python programs in a package.)

Numeric Simulation

Data Description

We use functions \(m_1\) \(m_2\), and \(m_3\) present three component functions. gene_data generates data from distributions. gene_grid_data generates data from the grid. Concretely, the response are generated by: \[ y = m(X) + \epsilon, \] where \[ m(X) = m_1(X_1) + m_2(X_2) + m_3(X_3) = \frac{8}{4 + X_1} + \frac{\exp(3-X^2_2)}{4} + 1.5\sin(\frac{\pi}{2}X_3), \] and \(\epsilon\) follows \(N(0, \sigma^2)\), the variance is \(\sigma^2=0.25\).

  • Case1: (gene_data parameter distribute = "normal") \(x\) generates from truncated multivariate normal distribution \(TN(0, \Sigma, -2, 2)\) , with mean zero and covariance matrix \(\Sigma=(0.3^{\mathbb{1}(i \ne j)})\) , and each predictor lies in \([-2, 2]\). (use function TruncatedNormal::rtmvnorm. )

  • Case2: (gene_data parameter distribute = "exp") \(x\) generates from truncated multivariate exponential distribution with same covariance matrix in case 1. The marginal distribution is exponential distribution with rate 1, and is truncated by 4 and translated to \([-2, 2]\). (use R package copula with function ellipCopula and rCopula. )

There two test data sets:

  • Grid: The grid are consist of \(10^6\) points with each predictor spanning at 100 evenly spaced points in \([-1.75, 1.75]\).

  • Distribution: random sample with 5000 points generated from the same distribution as the full data.

m1 <- function(x) {
  8 / (4 + x)
}

m2 <- function(x) {
  exp(3 - x^2) / 4
}

m3 <- function(x) {
  1.5*sin(pi / 2 * x)
}

trans_exp_data <- function(density, lower, upper) {
  out <- qexp( pexp(lower) + density*(pexp(upper) - pexp(lower)) )
  return(out)
}

gene_data <- function(N, rho, lower, upper, sd, distribute = "normal") {
  cov <- matrix(rho, 3, 3) + diag(1-rho, 3)
  if (distribute == "normal") {
    x <- TruncatedNormal::rtmvnorm(N, rep(0, 3), cov, lb = rep(lower, 3), ub = rep(upper, 3))
  } else if (distribute == "exp") {
    copula_def <- copula::ellipCopula(family = "normal", dim = 3, dispstr = "ex", param = rho)
    temp_quan <- copula::rCopula(N, copula_def)
    x <- apply(temp_quan, 2, trans_exp_data, 0, (upper-lower)) - (upper-lower)/2
  }
  
  colnames(x) <- c("X1", "X2", "X3")
  m <- 1 + m1(x[, "X1"]) + m2(x[, "X2"]) + m3(x[, "X3"])
  epi <- rnorm(N, 0, sd)
  y <- m + epi
  data <- as.data.frame(cbind(x, m = m , y = y))  
  return(data)
}
gene_grid_data <- function(lower, upper, one_dim_length, sd) {
  one_dim_seq <- seq(lower, upper, length.out = one_dim_length)
  x <- expand.grid(X1 = one_dim_seq, X2 = one_dim_seq, X3 = one_dim_seq, KEEP.OUT.ATTRS = FALSE)
  m <- 1 + m1(x[, "X1"]) + m2(x[, "X2"]) + m3(x[, "X3"])
  n_data <- nrow(x)
  epi <- rnorm(n_data, 0, sd)
  y <- m + epi
  data <- as.data.frame(cbind(x, m = m , y = y))
  return(data)
}

We write some auxiliary functions to implement cross validation(CV) and get evaluation measures.

  • ase computes average squared error

\[ \text{ASE}= \sum_{x \in \mathcal{X}_{test}} (\hat{m}(x)-m(x))^2 / \left| \mathcal{X}_{test} \right| \]

  • mee computes maximum estimation error:

\[ \text{MEE} = \max_{x \in \mathcal{X}_{test}} \left| \hat{m}(x) - m(x) \right| \]

  • create_folds create folds for CV.

  • get_opt_h get the optimal bandwidth (in fact is span parameter in function gam::gam).

    • This is the most time-consuming step in the entire procedure. I had try to use apply to substitute for loop in get_opt_h , it didn’t lead to significant improvements.

    • If handle_outlier=TRUE, find the index of the first occurrence of the maximum and minimum values from each predictor, and move these data from the test set to the training set.

  • get_result provide a unified surface to get MEE and ASE in the two test data sets.

The full data size is \(N=10000\) with \(p=3\) predictors. Hyper-parameter is set to \(q=16\). The bandwidth is searched in \(\{0.05, 0.1, \dots, 0.95\}\) for every predictor and chosen by five-fold CV. Each method are trained on subsamples \(n=1000\) , and evaluated on the two test sets with size \(10^6\) (grid) and 5000 (distribute).

N <- 10000; n <- 1000; test_distribute_num <- 5000; 
p <- 3; lower <- -2; upper <- 2; rho <- 0.3; sd = 0.5; K <- 5;
one_dim_seq <- seq(0.05, 0.95, length.out = 10)
h_grid <- expand.grid(one_dim_seq, one_dim_seq, one_dim_seq, KEEP.OUT.ATTRS = FALSE)

To save time, We repeat the simulation \(S=5\) times.

  • In each simulation we generate new full data and new test data.

    Although both IES and LowCon carry randomness (IES due to random selection of initial values and LowCon due to the initial space-filling design being randomly constructed). However, the randomness is not significant, it can be approximated to a deterministic approach, so the dataset is considered here to be regenerated each time.

    We tried using the same dataset across simulations and found that similar results were obtained, but IES consistently outperforming the other methods on MEE and ASE.

  • LowCon need a space-filling design, we may need try to use the different initial designs.

    Here for LowCon we used the lhs::randomLHD function to generate the space-filling design. The original IES simulation used the Sobol sequence to generate the space-filling design (spacefillr::generate_sobol_owen_set). Sobol seems better, at least need less time implies faster convergence.

Here for LowCon we used the randomLHD function to generate the space-filling design, the original IES simulation used the Sobol sequence to generate the space-filling design. Upon our attempts we found that there is little difference in the effectiveness of these two initial designs.

The package pbmcapply which based on parallel but provides progress bar to monitor the running process. The pbmcapply::pbmclapply function runs in forking mode on 5 cores (forking approach only works on POSIX systems (Mac, Linux, Unix, BSD) and not Windows).

We didn’t consider extrapolation in numeric simulation. Although the support of the model based on subsamples is smaller, the range of the grid test set is set far away from the boundary, and it is unlikely to be outside the boundary. The distributed test set is similar to the training set, and there are fewer points at the boundary. There won’t be a huge error.

Case 1: Truncated Normal Distribution

We compute the simulation result in case 1 and plot barplots of MEE and ASE in the two test datasets based on three subsampling methods:

test_grid <- gene_grid_data(lower = -1.75, upper = 1.75, 
                            one_dim_length = 100, sd = 0.25)
get_combine_result <- function(i) {
  data_train <- gene_data(N, rho, lower, upper, sd, "normal")
  test_distribute <- gene_data(test_distribute_num, rho, lower, upper, sd, "normal")
  rbind(get_result("Unif", data_train, n, K, h_grid, test_distribute, test_grid),
        get_result("LowCon", data_train, n, K, h_grid, test_distribute, test_grid),
        get_result("IES", data_train, n, K, h_grid, test_distribute, test_grid))
}

Case1_time_start <- Sys.time()
result_case_1 <- parallel::mclapply(1:5, get_combine_result, mc.cores = 5)
print(Sys.time() - Case1_time_start)
#> Time difference of 19.1164 mins
result <- do.call(rbind, result_case_1) %>% 
  as.data.frame() %>% 
  dplyr::mutate(dplyr::across(!Method, as.double),
         Method = factor(Method)) %>% 
  tidyr::pivot_longer(!Method, names_to = "Measure", values_to = "Value")

Distribution Testset

MEE in distribution test set:

ggplot(data = dplyr::filter(result, Measure == "MEE_distribute"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case1_MEE_Distribute")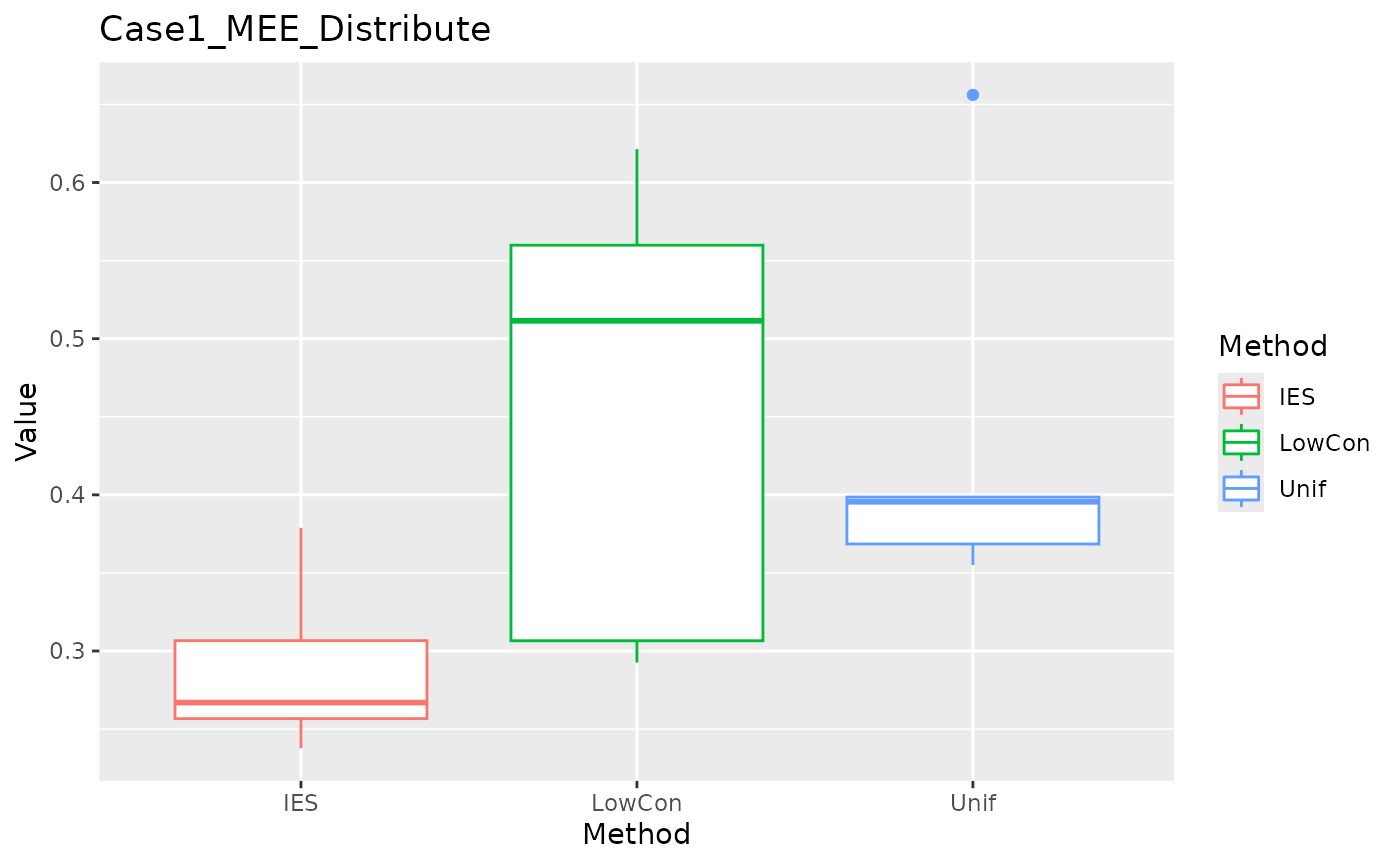

ASE in distribution test set.

ggplot(data = dplyr::filter(result, Measure == "ASE_distribute"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case1_ASE_Distribute")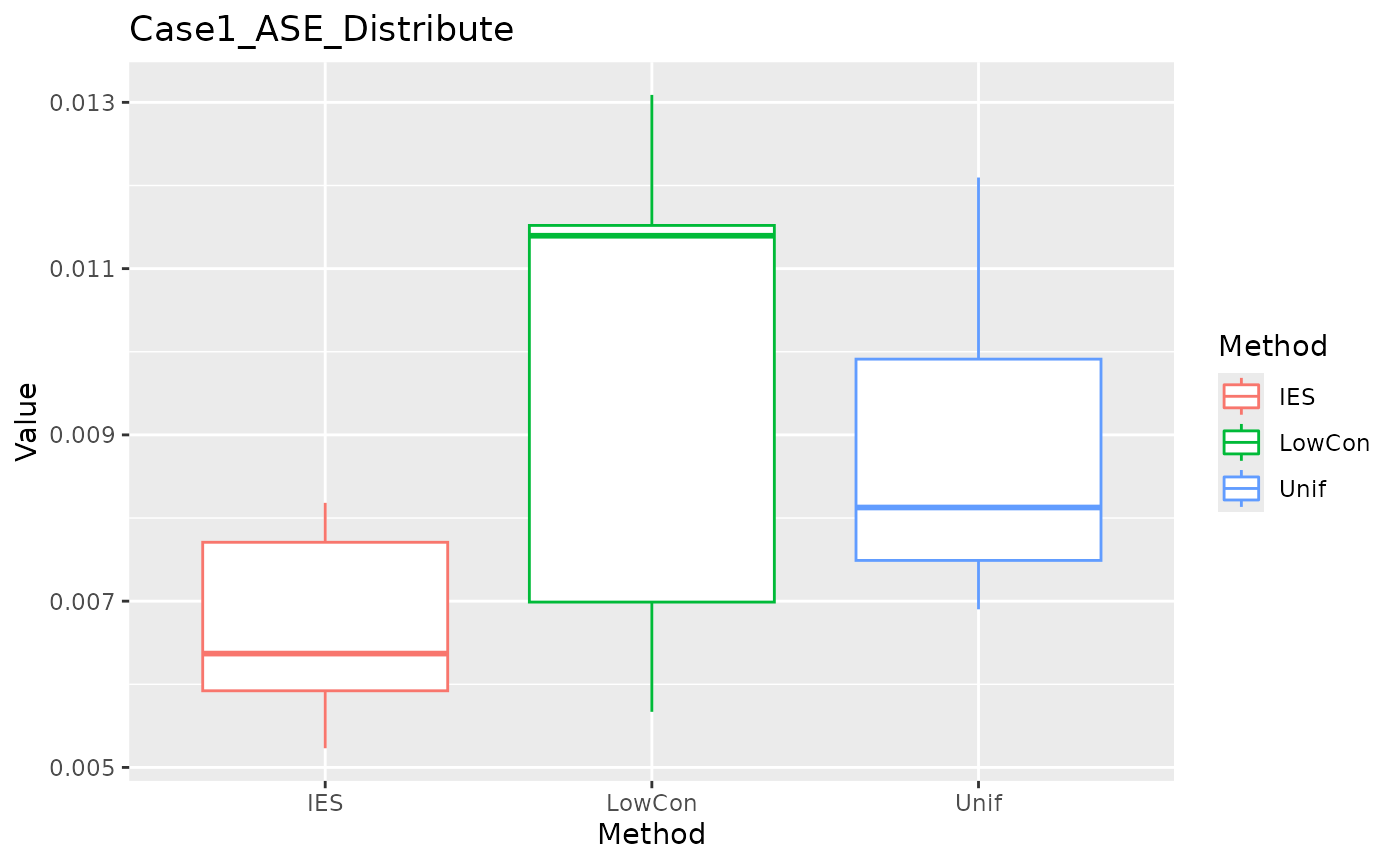

Grid Testset

MEE in grid test set.

ggplot(data = dplyr::filter(result, Measure == "MEE_grid"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case1_MEE_Grid")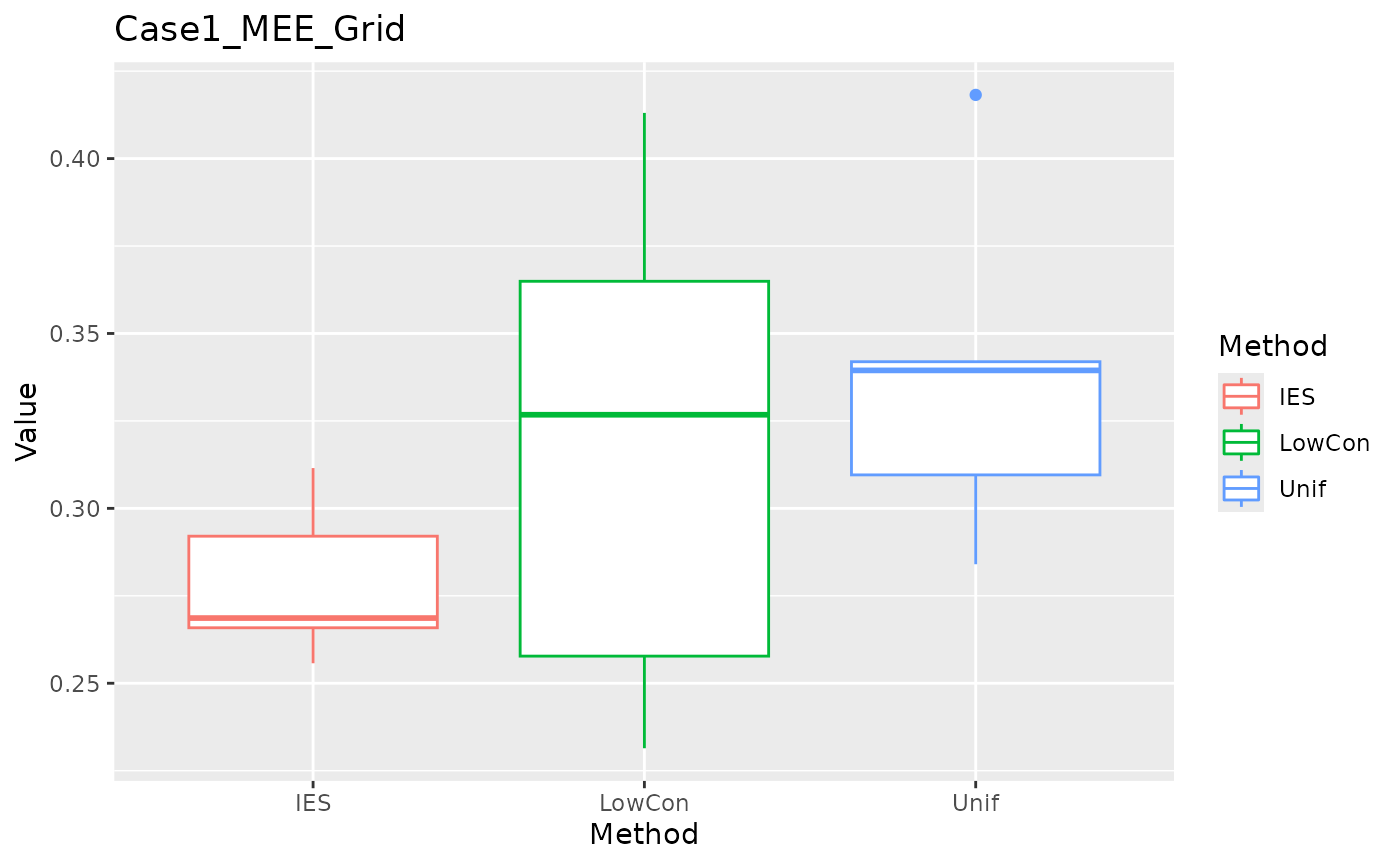

ASE in grid test set.

ggplot(data = dplyr::filter(result, Measure == "ASE_grid"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case1_ASE_Grid")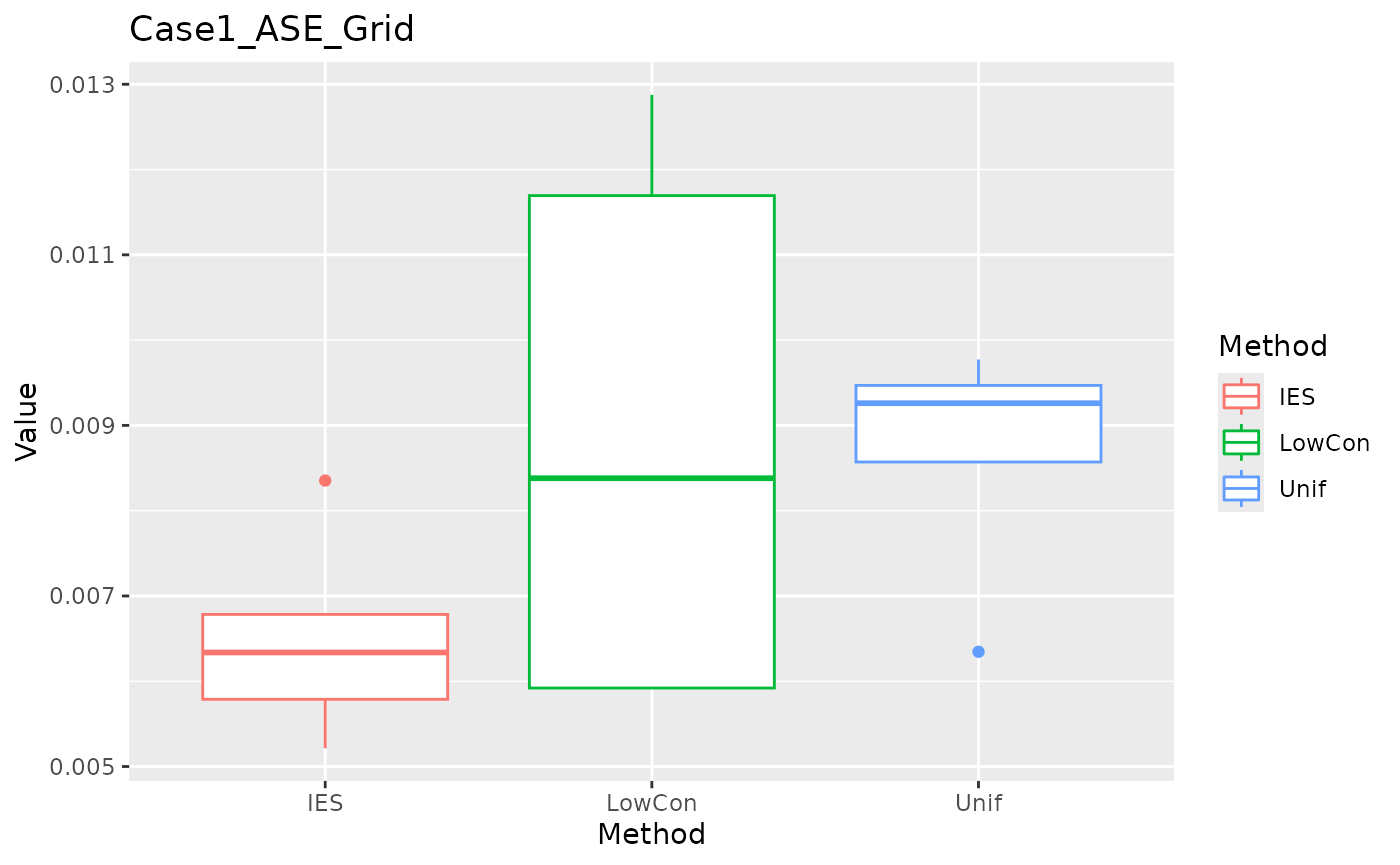

We can see that IES performs consistently well on MEE, but slightly worse on ASE. This is reasonable given the nature of IES itself.

Case2: Truncated Exponential Distribution

We compute the simulation result in case 2 and plot barplots of MEE and ASE in the two test datasets based on three subsampling methods.

get_combine_result <- function(i) {
  data_train <- gene_data(N, rho, lower, upper, sd, "exp")
  test_distribute <- gene_data(test_distribute_num, rho, lower, upper, sd, "exp")
  rbind(get_result("Unif", data_train, n, K, h_grid, test_distribute, test_grid),
        get_result("LowCon", data_train, n, K, h_grid, test_distribute, test_grid),
        get_result("IES", data_train, n, K, h_grid, test_distribute, test_grid))
}

Case2_time_start <- Sys.time()
result_case_2 <- parallel::mclapply(1:5, get_combine_result, mc.cores = 5)
print(Sys.time() - Case2_time_start)
#> Time difference of 22.27652 mins
result <- do.call(rbind, result_case_2) %>% 
  as.data.frame() %>% 
  dplyr::mutate(dplyr::across(!Method, as.double),
         Method = factor(Method)) %>% 
  tidyr::pivot_longer(!Method, names_to = "Measure", values_to = "Value")

Distribution Testset

MEE in distribution test set:

ggplot(data = dplyr::filter(result, Measure == "MEE_distribute"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case2_MEE_Distribute")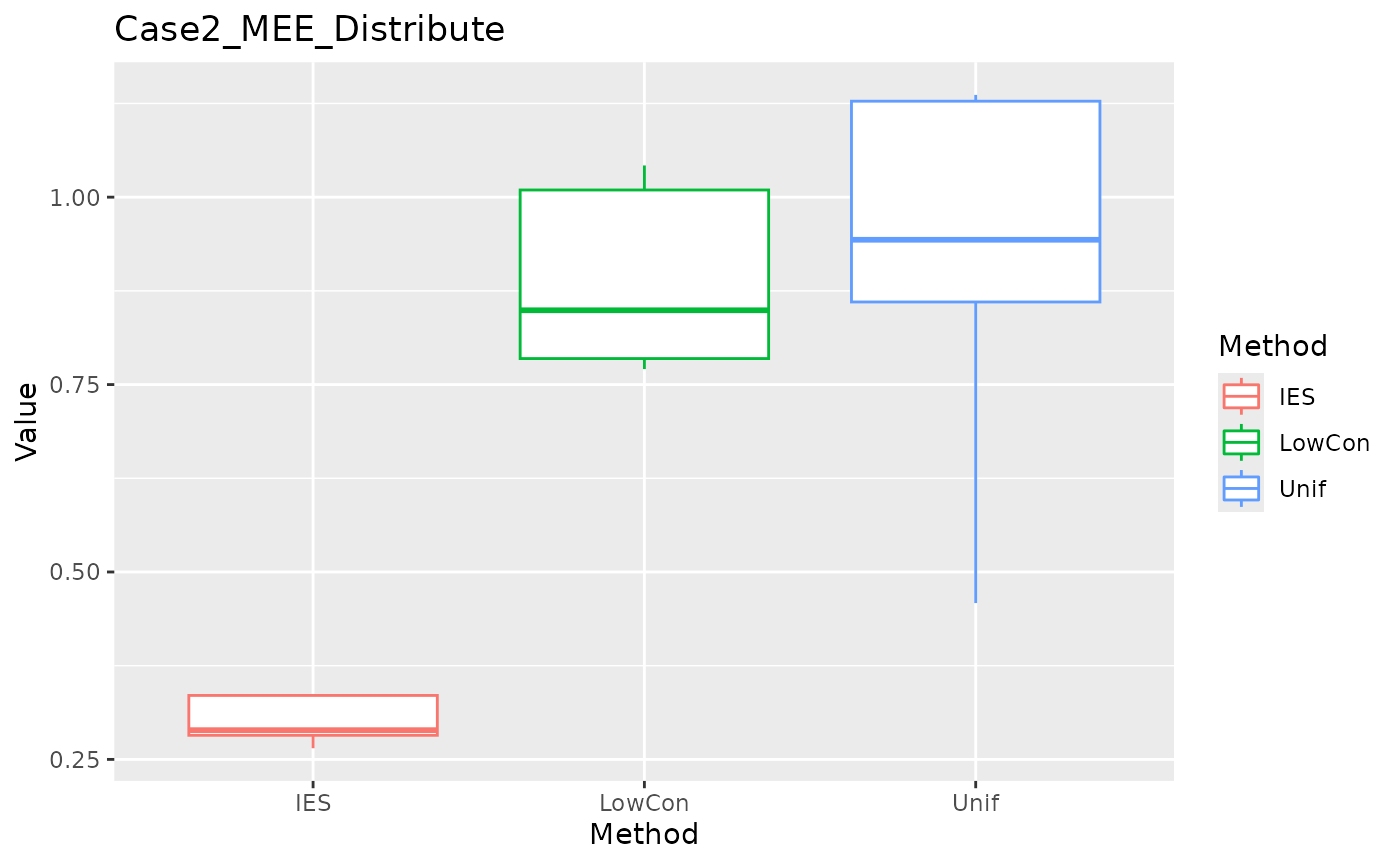

ASE in distribution test set:

ggplot(data = dplyr::filter(result, Measure == "ASE_distribute"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case2_ASE_Distribute")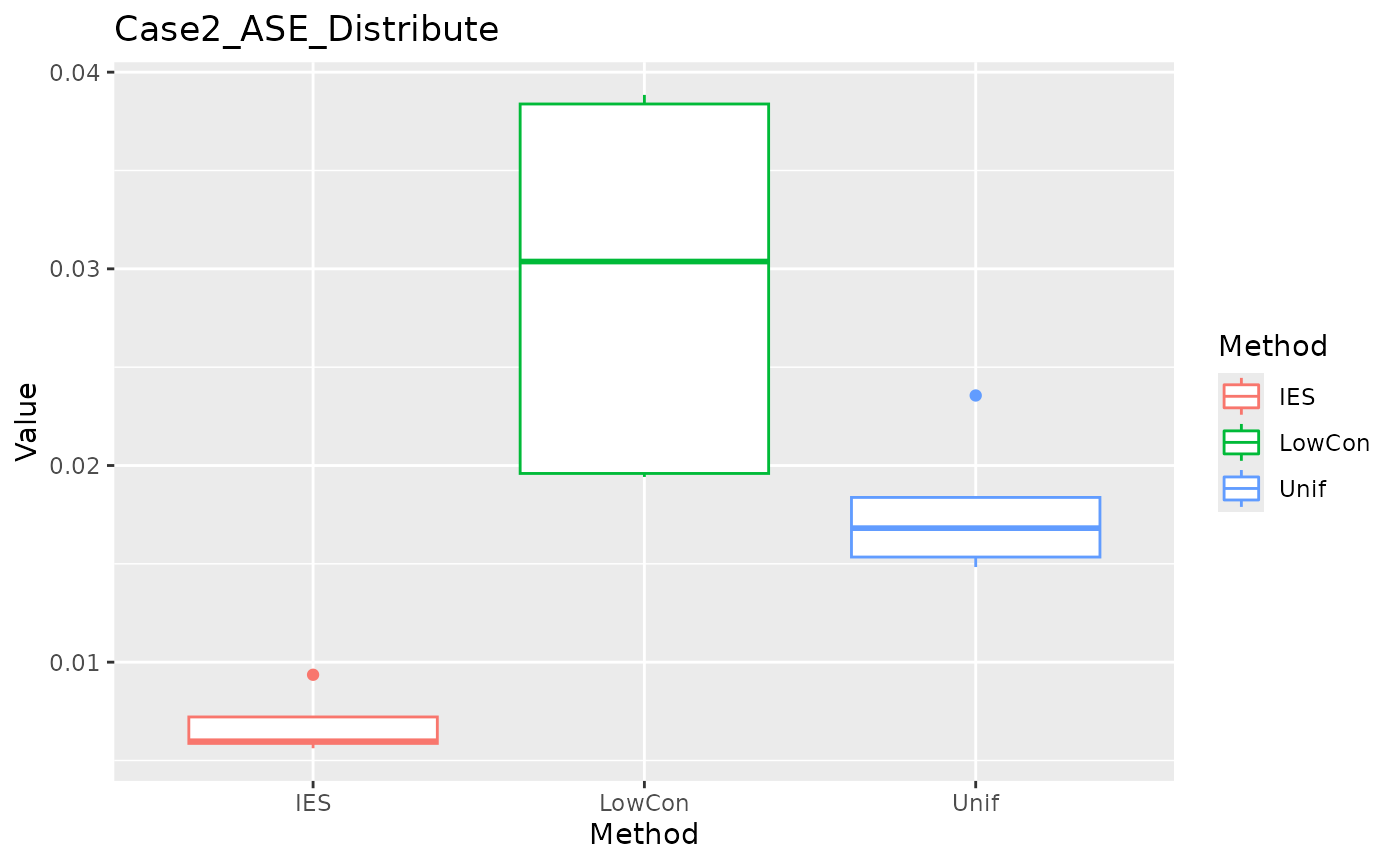

Grid Testset

MEE in grid test set.

ggplot(data = dplyr::filter(result, Measure == "MEE_grid"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case2_MEE_Grid")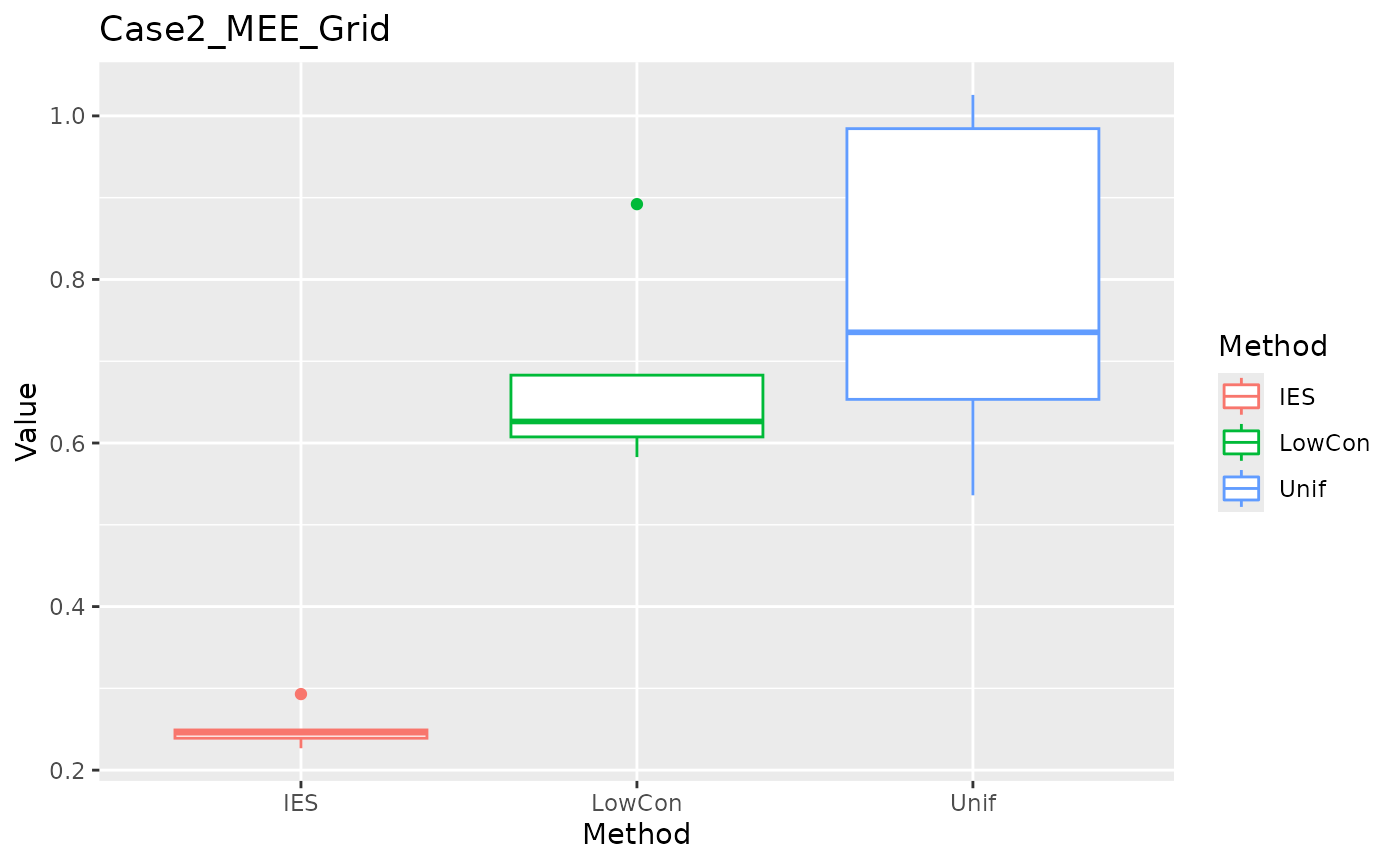

ASE in grid test set.

ggplot(data = dplyr::filter(result, Measure == "ASE_grid"), aes(x = Method, y = Value, color = Method)) + 
  geom_boxplot() + ggtitle("Case2_ASE_Grid")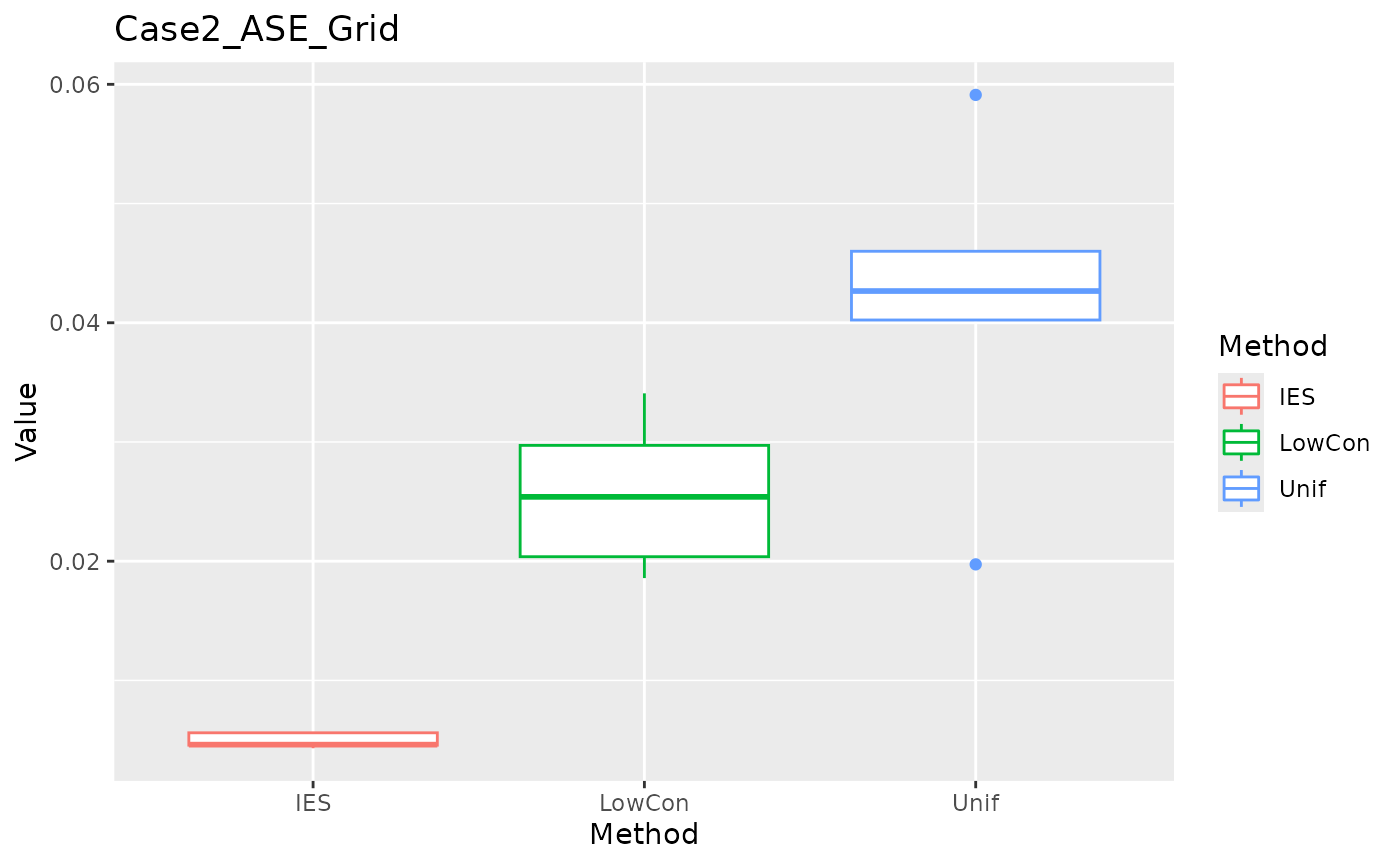

In the Case2 exponential distribution, IES performs consistently well on both MEE and ASE. This implies IES performs better in biased distribution?

Real Case

Description

We use the diaomonds data set inggplot2 package. Involving three numeric variables carat, depth and table as predictors, set price as response and implement log transform to carat and price.

real_train <- ggplot2::diamonds |>
  dplyr::filter(x !=0 & y != 0 & z != 0) |>
  dplyr::select(carat, depth, table, y = price) |>
  dplyr::mutate(carat = log(carat), y = log(y))

We get four models based on the full data and three subsample methods (set \(n=5000\) ) to observe the estimation of the component functions. We still use five-folds cross validation to get the optimal bandwidth and the search space is same as numerical simulation. Hyper-parameter is stall set to \(q=16\).

When get the optimal bandwidth, we set the handle_outlier=TRUE. This ensures that the boundary of each predictor in the training set has a value, otherwise the range of application of the model is too small, resulting in poor results. (In numeric simulation, we didn’t consider handle outliers)

N <- nrow(real_train); n <- 5000;
q = 16; K = 5; x_name <- c("carat", "depth", "table")
one_dim_seq <- seq(0.05, 0.95, length.out = 10)
h_grid <- expand.grid(one_dim_seq, one_dim_seq, one_dim_seq, KEEP.OUT.ATTRS = FALSE)

index <- list(
  Full = 1:N,
  Unif = sample(1:N, n),
  LowCon = dbsubsampling::LowCon(real_train[,c("carat", "depth", "table")], n, theta=1),
  IES = dbsubsampling::IES(real_train[,c("carat", "depth", "table")], n, q))

real_cv_time <- Sys.time()
h_opt <- purrr::map(index, 
                    function(.index) 
                      suppressWarnings(
                        get_opt_h(h_grid, real_train[.index,], K, 
                                  x_name = x_name, y_name = "y",
                                  handle_outlier = TRUE)))
print(Sys.time() - real_cv_time)
#> Time difference of 14.18193 mins

Estimate component function

We use gam::predict.Gam function and set the parameter type = "terms" to get the estimation of regression function of each predictor. And after obtaining the estimate we centralize each regression function.

Here we use two sets for testing, one with the training set itself as the test set, and the other consisting of a grid of three variable values. (\(50 \times 50 \times 50\) points in \([-1.6, 1.6] \times [43, 79] \times [43, 95]\))

Due to the small sample size of the subsample, the model fitted on it has a small scope of application, we extrapolated the values outside the scope (use termwise nearest neighbor estimation, in fact, is to replace the values outside the boundary with the boundary values). Estimates outside the boundary are very inaccurate without extrapolation, especially for Unif and LowCon (IES have wider boundaries due to one-dimensional uniformity).

get_interval <- function(data, index, x_name) {
  x <- data[, x_name]
  subdata <- x[index, ]
  interval <- apply(subdata, 2, range)
  return(interval)
}

extrapolation <- function(data, interval, x_name) {
  x <- data[, x_name]
  for (j in 1:ncol(x)) {
    x[,j][x[,j] < interval[1,j]] <- interval[1,j]
    x[,j][x[,j] > interval[2,j]] <- interval[2,j]
  }
  data[, x_name] <- x
  return(data)
}

model <- purrr::map2(h_opt, index, function(.h, .index) {
  opt_formula <- formula(y ~ 
                           lo(carat, span = .h[1], degree = 1) + 
                           lo(depth, span = .h[2], degree = 1) + 
                           lo(table, span = .h[3], degree = 1))
  gam::gam(opt_formula, data = real_train[.index,])
})

interval <- purrr::map(index, function(.index) 
                                get_interval(real_train, .index, x_name))

extrapolation_ori_data <- purrr::map(interval, 
                                function(.interval) 
                                  extrapolation(real_train, .interval, x_name))
predict_ori_data <- purrr::map2(model, extrapolation_ori_data, 
                                function(.model, .data) 
                                  predict.Gam(.model, .data, type = "terms"))

real_grid <- expand.grid(carat = seq(-1.6, 1.6, length.out = 50),
                         depth = seq(43, 79, length.out = 50),
                         table = seq(43, 95, length.out = 50),
                         KEEP.OUT.ATTRS = FALSE)

extrapolation_grid_data <- purrr::map(interval, 
                                function(.interval) 
                                  extrapolation(real_grid, .interval, x_name))
predict_grid_data <- purrr::map2(model, extrapolation_grid_data,
                                 function(.model, .data)
                                   predict.Gam(.model, .data, type = "terms"))
ori_predict <- predict_ori_data %>% 
  purrr::map(scale, center = TRUE, scale = FALSE) %>% 
  purrr::map(as.data.frame) %>% 
  purrr::map(rename, y_carat = "lo(carat, span = .h[1], degree = 1)",
                     y_depth = "lo(depth, span = .h[2], degree = 1)", 
                     y_table = "lo(table, span = .h[3], degree = 1)") %>%
  dplyr::bind_rows(.id = "Method") %>% 
  tibble::remove_rownames() %>% 
  cbind(rbind(real_train, real_train, real_train, real_train)) %>% 
  dplyr::rename(x_carat = carat, x_depth = depth, x_table = table) %>%
  dplyr::select(-y) %>% 
  tidyr::pivot_longer(!Method, names_to = c(".value", "Variable"), names_sep = "_")

grid_predict <- predict_grid_data %>% 
  purrr::map(scale, center = TRUE, scale = FALSE) %>% 
  purrr::map(as.data.frame) %>% 
  purrr::map(rename, y_carat = "lo(carat, span = .h[1], degree = 1)",
                     y_depth = "lo(depth, span = .h[2], degree = 1)", 
                     y_table = "lo(table, span = .h[3], degree = 1)") %>%
  dplyr::bind_rows(.id = "Method") %>% 
  tibble::remove_rownames() %>% 
  cbind(rbind(real_grid, real_grid, real_grid, real_grid)) %>% 
  dplyr::rename(x_carat = carat, x_depth = depth, x_table = table) %>%
  tidyr::pivot_longer(!Method, names_to = c(".value", "Variable"), names_sep = "_")

We plot the estimate of three component functions on distribution test set. We can see that LowCon performs the worst and is close to non-convergence. Unif also performed poorly, especially at the border. IES performed the best and most closely with the full sample.

ori_predict %>% 
  ggplot(aes(x = x, y = y, group = Method, color = Method, linetype = Method)) +
  geom_line() +
  facet_wrap(~Variable, scales = "free") +
  ggtitle("Component function estimation on the original data.")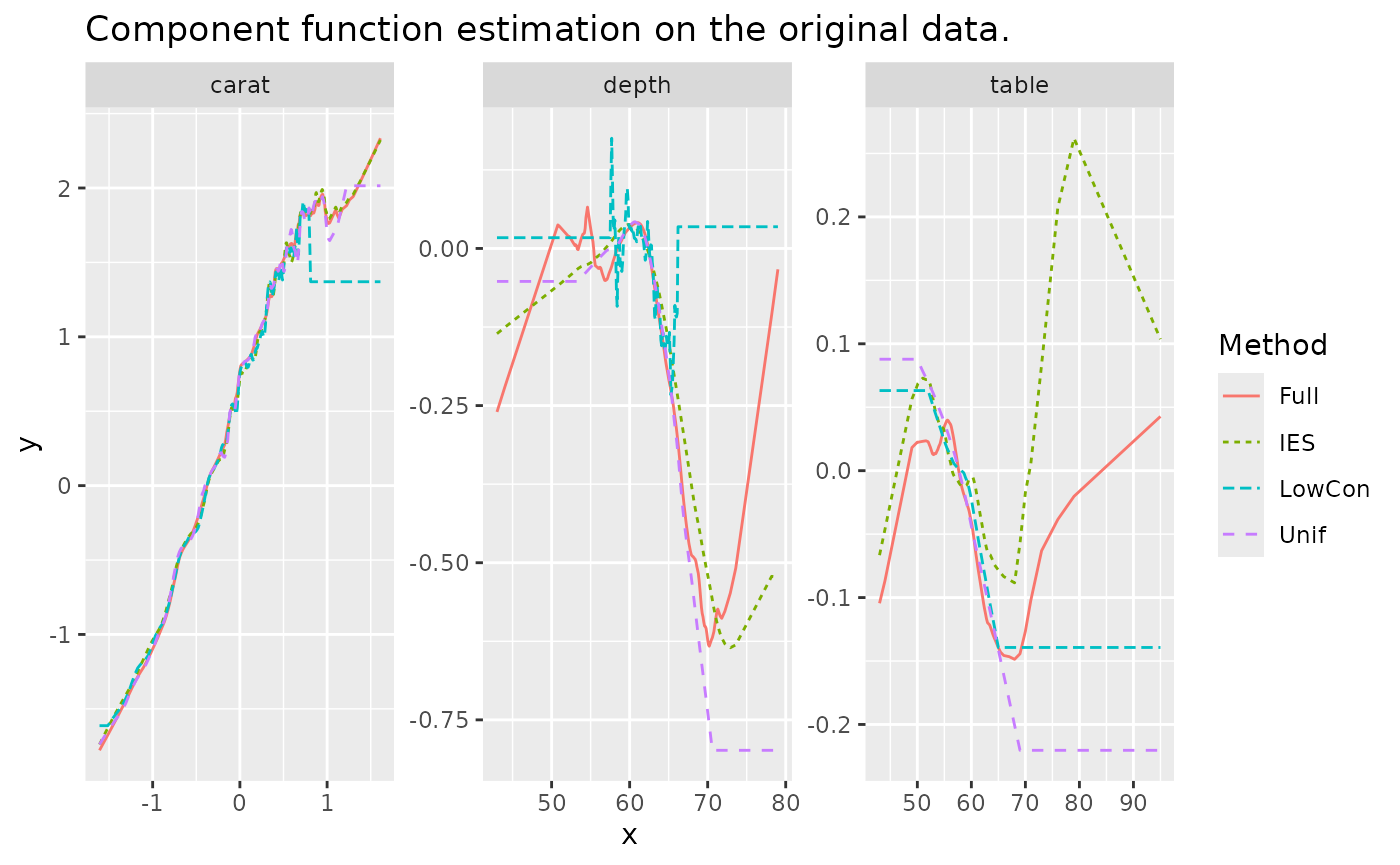

And the estimate of three component functions on grid testset which has similar performance with distribution testset.

grid_predict %>% 
  ggplot(aes(x = x, y = y, group = Method, color = Method, linetype = Method)) +
  geom_line() +
  facet_wrap(~Variable, scales = "free") +
  ggtitle("Component function estimation on the grid.")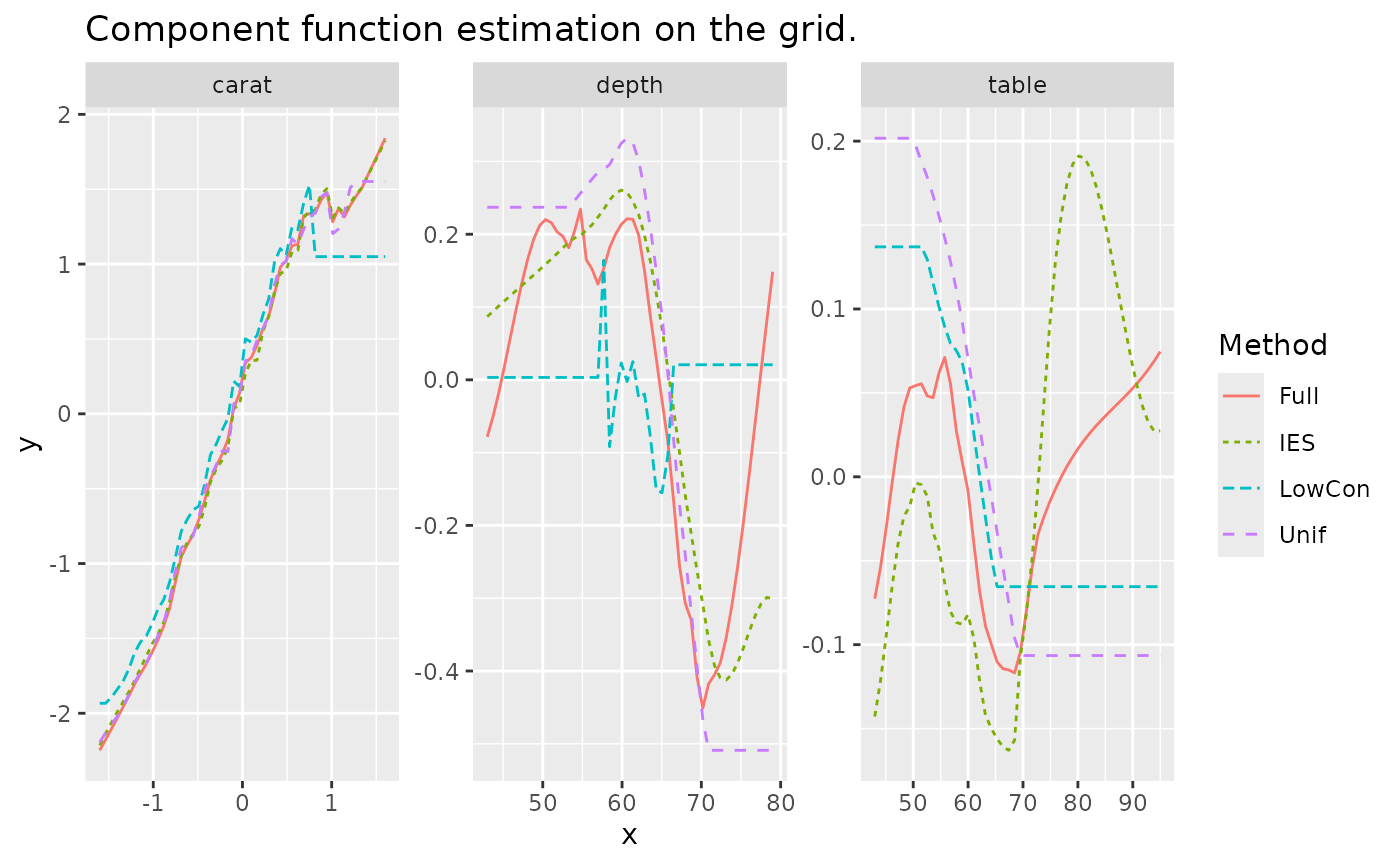

Compute measures

We compare the MEE and ASE on the grid and original data under models based on different subsample and full data. There is no real response on the grid test set, so we use the estimate obtained from the model based on full data as the response.

Extrapolation is carried out not only when drawing graphs, but also when calculating measures, otherwise the values of MEE and ASE will be extremely large (especially LowCon and Unif).

y_ori <- real_train[["y"]]
y_grid <- predict.Gam(model[["Full"]], real_grid)
predict_extra_ori <- purrr::map2(model, extrapolation_ori_data, predict.Gam)
predict_extra_grid <- purrr::map2(model, extrapolation_grid_data, predict.Gam)

extra_measure <- bind_cols(
  Measure = c("MEE_Ori", "ASE_Ori", "MEE_Grid", "ASE_Grid"),
  dplyr::bind_rows(purrr::map_dbl(predict_extra_ori, mee, y_ori),
                   purrr::map_dbl(predict_extra_ori, ase, y_ori),
                   purrr::map_dbl(predict_extra_grid, mee, y_grid),
                   purrr::map_dbl(predict_extra_grid, ase, y_grid))) %>%
  tidyr::pivot_longer(!Measure, names_to = "Method", values_to = "Value")

extra_measure %>% 
  ggplot(aes(y = Method, x = Value)) +
  geom_bar(stat = "identity") +
  facet_wrap(~Measure, scales = "free")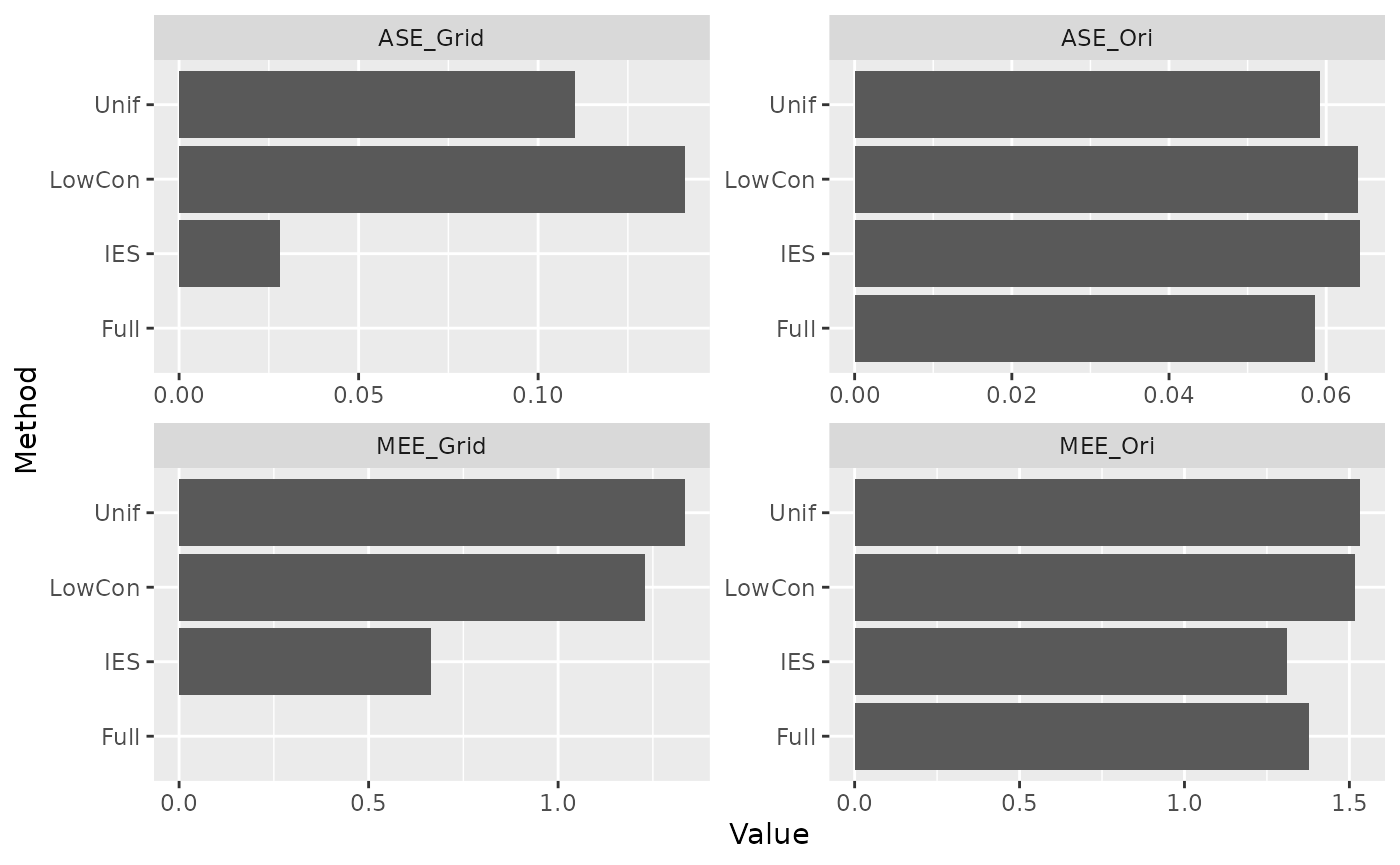

IES performed consistently well on MEE. ASE performs better on the grid test set and worse on the distribution test set (possibly due to data leakage). This is in line with our expectations.

We have reproduced only some of the IES simulations here, and others are subject to subsequent refinement.